tech
ハッカーの遺言状──竹内郁雄の徒然苔
第18回:問題児も悪くない
元祖ハッカー、竹内郁雄先生による書き下ろし連載の第18回。今回のお題は「問題児も悪くない」。
ハッカーは、今際の際(いまわのきわ)に何を思うのか──。ハッカーが、ハッカー人生を振り返って思うことは、これからハッカーに少しでも近づこうとする人にとって、貴重な「道しるべ」になるはずです(これまでの連載一覧)。
文:竹内 郁雄
カバー写真: Goto Aki

「栴檀は双葉より芳し」という諺がある。栴檀とは白檀の別名で、この諺は、白檀は双葉、つまり発芽のときから香気があることから、大物は幼いころからそれを示しているということである。私の場合は、「毒だみは双葉より臭し」という諺が相応しい。
小学3年のころ、私は8÷8が0だと言ってきかず、担任の先生を困らせたらしい。いや、「らしい」ではなくては、自分にも記憶があるので、「困らせた」である。もし、いまこんなことを頑固に主張する子がいたら、先生としてはどう教えたものだろう。私は何を間違えたか大学は数学を専攻したのであるが、自分のことは棚に上げて厄介な問題だと思う。
私のすぐ上に6歳年上の兄がいて、年が離れているのにとてもよく相手してくれた。ピンポン、バドミントン、軟式テニスボールと竹バットを使った野球(生まれがお寺なので、子どもにとっては広い境内でピッチャーとバッターを交代して2人だけでも遊ぶことができた)。私に水準以上の運動能力がついたのはこのおかげだと思う(※1)。境内の形のせいで、バッターは左打席が自然だったので、兄も私も右利ききなのにバッティングだけは左だった。そのおかげで大人になってから右左どちらの打席にも立つことができたが、私は左目の視力が弱かったので、左打席のほうが打率は良かった。
その兄が塾から帰ってきて教えてくれたのが次の問題である。私が多分小学6年のときなので、1958年である。マーティン・ガードナーがScientific Americanにこの問題を紹介したのが1957年だから(※2)、いま思うにこの塾の先生、すごいと思う。
とある会社の社長は毎日午後5時に会社を出て自宅からの迎えのクルマに乗って帰る。
ある日、午後4時に退社した。
天気が良かったので、迎えのクルマに出会うまで散歩した。
出会ったところで、クルマはUターンして自宅に戻った。
するといつもより10分早く帰宅した。
何時何分にクルマに出会ったか?
8÷8が0だと言ってきかなかった私にもこの問題は面白いと思った。そのときは当然まったく思い至らなかったが、まともに解こうとすると、社長やクルマの速度だの、会社と自宅の距離だの、自宅を出発する時刻だの、やたらと変数の多い連立方程式を解かないといけない。しかし、ある簡単な考え方に思い至ればこの問題は一瞬で解ける。小学生でも「Aha!」だ。素晴らしい問題である。
「毒だみは双葉より臭し」なので、自分でもこんな面白い問題を作れないかとボーッと考え続けたことが割と鮮明に記憶に残っている。なんか浮輪の中だか表面だかを何かが動いているような問題を一所懸命考えていた。もちろん、問題らしいものは作れなかった。ま、そんなものでしょう。
そして激しく時代は下る。数学科で「できない竹内」の異名をもっていた私は、大学院の数学専攻で、中公新書の「詭弁論理学」や「逆説論理学」で有名な野崎昭弘先生のオートマトンに関する講義を聞いた。しかし、さっぱり分からなかった。いま思っても分かって然るべきだったと思うのだが、野崎先生、数学専攻での講義ということで、気合いを入れて思いきり抽象的な話に仕立てたのではないかと思う(あくまでも思う、である──何しろ45年前の話だ)。
講義を受講すれば試験がある。これは論理学を引き合いに出さずとも、当然の帰結である。さすがにある程度は解けたが、どうしても解けない問題がある。うーむ、これは「それはさておき」法しかない。
というのには理由がある。大学1年生のころ、経済学の講義(いま思うにサムエルソンの経済学)を聞いたのだが、さっぱり分からない。何がどう分からなかったのかは当然のことながら覚えていないが、簡単な等式の右辺の1項を左辺に移項した途端に、鬼の首でも取ったかのように新しい解釈が生まれるという独特のやり方にまったく馴染めなかったのだろう、と朧げながら記憶している。
学生寮で仲良くしていただいた先輩で経済学部の人がいた。この人に「分からん」ということを打ち明けたら、じゃこれを見ておくといいと言って薄い本を貸してくれた。薄いから、まぁなんとか読める。残念ながら、その著者の名前を忘れてしまったが、経済学の試験で、解けない問題に「それはさておき、最近読んだ○○の本によれば……」と書いたのが大成功で、先生に呼ばれて「大学1年生なのに、よくこんな本を知っているな」と質問されて、しょうがないので正直に答えたら、「優」をもらえてしまった。これを思い出したわけである。
野崎先生の試験に、おもむろに「それはさておき」と書き始めて、書いたのが次の問題である。試験とは答えるべきものなのに、自分には解けていなかった創作問題を書いたのだ。毒だみの面目躍如である。
平面上の図形(点集合)でどの直線とも正確に2点で交わるものはあるか?
たった1行だが、問題は短いほど迫力がある。試験に答えられなかったくせになんとも生意気な話だが、ともかく単位の首の皮はつながった。
一応、この問題の「面白さ」を解説しておこう。例えば、よくご存知の平行2直線。これはこの直線に平行でないどの直線ともきちっと2点で交わる。惜しい! では、とても大きな円。これもその円の内部を通る直線とは2点で交わる。この円、とても大きいんだけどなぁと言っても無駄。その外の直線とは交わりもしない。平行でない2直線(これは一般の双曲線が縮退したものと思うこともできる)も、ほとんどの直線とは2点で交わる。どうもちょっと思いつく単純な図形じゃ、どうもだめらしい。
落ちこぼれ数学生の私がコンピュータプログラミングの道に逃げてからは、数学専攻の中で特異な存在になってしまい、逆にその分、あまりひけ目を感じずに先生方、先輩、同級生とお付合いできるようになった。思うに、これは戦略ではありますね。そんなあるとき、ひょんなことから、この「それはさておき問題」がお茶飲み場で話題になった。いらっしゃった大先生方も「うーん、結構難しいね。でも、解けない問題ではないはずだ」というところでお仕舞い。いやぁ、答えが「存在する」「存在しない」の2通りしかない未解決問題を創作できたとは、とちょっと嬉しくなったものだ(※3)。
その後、野崎先生にはいろいろお世話になり、黎明期の人工知能の教科書の翻訳のお手伝いをしたこともあった。また数学科に、コンピュータに触る後輩が出てきて、肩身の狭い思いをしなくてよくなった。特に2人の後輩、後藤滋樹さん(早大教授)と佐藤雅彦さん(京大名誉教授)とは、いろいろなところで話が合い、ご縁もあって親しくさせていただいた。
その佐藤雅彦さんが、たしか京都に出かける新幹線の中で一緒だったとき、くだんの「それはさておき問題」が難波完爾先生の教科書の演習問題に出てましたよ、と教えてくれた。えっ、超かっこいい創作未解決問題が教科書の演習問題に? その後分かったのだが、この問題はフラクタル図形の典型例(図1)で有名なシェルピンスキーが提唱した問題だったとか!
図1:シェルピンスキーのガスケット。Wikipediaより引用。見て分かるように再帰的に同じ図形がある手続きの繰り返しの中で小さくなっていく。この図形は5回まで繰り返したところ。これを本来は無限回繰り返す。
というわけで、またも毒だみの本性を暴露してしまった。なお、演習問題の解答によれば、このような点集合は存在する。実際に「超元気農法」もとい、「超限帰納法」によって「構成的」に描ける。と言われても、超限帰納法なので、現実的に描くことはできない。つまり、平面上に雲霞のように散らばった点の集合になるので、目に見えない。こうなると「そのような点集合があると言われてもねぇ」という気分になる。北斗七星の中のベネトナッシという名の恒星の第3衛星にものすごい金の鉱脈が存在すると言われたようなものだ。
毒だみの繁殖力はすごい。毒のように見えて解毒材にもなる。毒をもって毒を制すなのだろうか。そんなわけでいまだに死にきれずに遺言状を書き散らしている。
社会人になっても、「それはさておき」はさておき、なんだかんだと問題を起こしていた私であったが、たまにはちゃんとした問題を作ることがあった。解くべきというより、コンピュータに解かせる速度を競うための問題、すなわちベンチマークテストの創作である。こういうのを真の問題児というのだろう。
1970年代前半、自然言語処理システムの研究から、それを支えるためのLisp言語システムの開発に体重を移した私が加わった研究コミュニティがあった。1977年には情報処理学会の記号処理研究会という正式の組織になったのであるが、それ以前は非公式なコミュニティだった。みんなLispという言語が大好きで、競って処理系を開発していた。競うからにはベンチマークテストが必要だ。当時のコンピュータパワーで走らせることができて、処理系ごとの得意不得意が分かるテストが良い。
ここで毒だみは考えた。ベンチマークテストはLisp言語で閉じたものではなく、ほかの言語に対してLispの能力の高さを示すものでなければならない。つまり、Lisp依怙贔屓ベンチマークを作らねば……。差をつけるとすれば、再帰、関数自体をファーストクラスデータとして扱えること(あるいは関数閉包)、リスト処理などであるが、すべてを追いかけてはいけない。というか、当時は再帰の性能で勝負するので十分だった。
再帰と言えば、アッカーマン(Ackermann)関数が抜群に有名であった。これはとんでもない関数で、2つの自然数(この場合0以上の整数)を与えたら1桁の自然数でもコンピュータの寿命どころか、宇宙が終焉を迎えるまで計算が終わらない。というか終わる前にメモリを食いつぶす。テラバイト、ペタバイト、ヘキサバイト、そんな生易しいものではまったく役に立たない。
1974年の夏前だったと思うが、アッカーマン関数ほど強面じゃなくて、単純だが、再帰の性能が試せるベンチマークをあれこれ考えていた。こうしてある日の午前、ふと思いついたのが、なんといまや私の名前がついた竹内関数である(※4)。ちょっと強面だが、次のように定義される関数である。関数の名前は当初私が名付けた tarai のままにしてある。本来はLispで書くべきかもしれないが、そこはぐっと抑えて……。
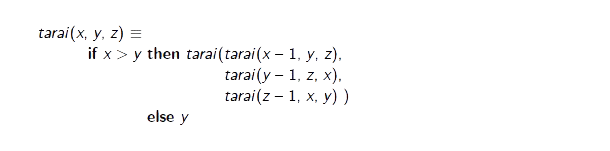
doronuma(x) ≡ doronuma(x-1)
も再帰的定義だが、これはすぐ分かるように無限に奈落に落ちていく堂々巡り。結局、何も定義できていない。tarai もこれで一体何かが定義できているのか、すぐには分からない。しかも、tarai を定義するのに、tarai を使うどころか、その tarai の引数の中でまた tarai を3回も呼んでいる。
ところがうまくしたもので、これはどんな整数 x, y, z を与えても、値が x または y または z になるのである。しかし、コンピュータにこの定義を与えると(※5)、恐ろしく時間がかかる。例えば、n を正の整数とすると
tarai(2n, n, 0)
は、ざくっと言って n の n 乗(nn)に比例した時間がかかる。例えば、n = 10 とすると n = 2 の場合の25億倍の時間がかかる! これだけの時間をかけて答えは 2n である。定義をチラリと眺めれば分かるように、大小比較で枝分かれするほかには、1を引く引き算と関数呼び出ししかしていないが、x, y, z の位置がクルクル回っている。これが tarai、つまりタライ回し関数と当初名付けた理由である。
竹内関数ことタライ回し関数は、アッカーマン関数に比べればヒヨコのヒヨコだが、それでも十分に時間がかかる。それでいて、計算の途中で使うメモリはほんのちょっとしかない。上の例では途中に現れる数は -1 から 2n の間の整数だし、計算に必要なスタックの長さは n の数倍程度である。洗濯機の中のマイコンでも計算できる。つまり、ベンチマークとしては無差別級として使える問題だったのだ。
この関数を思いつくのに要した時間は約2時間。しかし、いまはTakeuchi functionという名前で世界のコンピュータ科学研究者の数パーセントは知っているくらいに有名になってしまった。私が亡くなってもしばらくは教科書に残ることになると思う(※6)。
思えば、不思議なものだ。私は40年近く、一応コンピュータの分野で研究したり、真面目にシステムを作ったりしてきたのだが、たった2時間で思いついた関数1個だけが、没後しばらくの間は学界の記憶に留まるかもしれないということだ。どんなに品行方正な人でも、一瞬の事件で世間の記憶に残るのといい勝負のような気がする。
そういえば、このタライ回し関数の引数が整数でなくて、実数でも同じ意味になることを証明してくださったのが、前述の野崎昭弘先生だ(またも再帰)。1980年だと思うが丁寧に万年筆で書かれた、これまた3ページのお手紙をいただいた(写真3)。「それはさておき」が100倍のご褒美になって返ってきた気分である。
とはいえ、昔のことだし、本人はだいぶ記憶が薄れてしまっていたのだが、2012年、初音ミクの音楽で有名なクリプトン・フューチャー・メディアの音楽プログラマ、藍圭介さん(写真4)が、なんと竹内関数を音楽にしてくれた! 知る人ぞ知るミニマル音楽の大家スティーブ・ライヒ (Steve Reich)の音楽そっくりな雰囲気の音楽が自動生成されるのである。

写真4:藍圭介さん。この竹内関数音楽で、ニコニコ学会βで表彰された。
関数から音楽が生まれる仕掛けは、再帰呼び出しをするたび、3つの引数 x, y, z の値を音階の音(藍さんは分散和音にした)に対応させるというものだ。こうして、tarai(10, 5, 0) から343,073小節の音楽が作曲される。これがどうしてそれらしい音楽になるかの理由なども含めて、藍さんのブログを参照されたい。そこから抽出された60小節の音楽も聴ける。これで2分だから、全曲聴くと8日ほどかかる。究極のヒマ潰しになろう。
竹内関数で音楽生成
タライ回し関数の引数を変えて、違う作曲になることを聴けるページも用意されている。
Tarai Function Music
調べると、ほかに同様のことを試みている人がいるようだ。毒だみとしては世の中に功徳を施したのか、害悪をたれ流したのか……。
前回の「辭典の楽しみ」では、辞典を引く・読む楽しみもいいが、辞典を作る楽しみもあるということを紹介した。また、學問を学ぶのもいいが、學問を作るのも楽しいという話を機会あるごとに紹介している。その伝で、問題を解くのもいいが、問題を作る・生み出すのも楽しい、つまり、問題児も悪くないというのが今回の趣旨である。
大学教員という商売柄、いろいろな試験問題を作ったが、私は結構楽しんだほうである。日本評論社の雑誌「数学セミナー」の「エレガントな解答を求む」欄にもときどき出題しているが、私にとっては「エレガントな解答を求む」ではなく、「エレガントな問題を求む」である。これが結構難しい。何回か失敗もした。そんなわけで、楽しんでいるのか、悩んでいるのかが、分からなくなることがある。人生そんなものかもしれない。(つづく)
※1:実は、玄関から門まで30メートル弱の幅1.5メートルのコンクリートの道に一晩で平気で数十センチ積もる雪の雪かきが最も体力養成に役立ったと、いまになって思う。
※2:日経サイエンスの創刊は1971年。なお、つい最近出版された、岩沢宏和、上原隆平監訳「ガードナーの数学ゲーム全集1」(日本評論社)の第3章に紹介されている。
※3:そういえば、これは連続体仮説と連動しているのではないか、とおっしゃった先生がいた。もし、そうだとすると、これは存在しても存在しなくてもいいことになる。え、こんな子どもにも理解できる問題がそんな結末になるはずがない……。
※4:この命名は野崎先生が15年越しで完成させた教科書で初めて紹介された。野崎昭弘「計算機数学(共立数学講座 11)」(共立出版、1984)。
※5:このごろのプログラミング言語は再帰的定義ができないものを探すほうが難しい。
※6:Donald E. Knuth: Textbook Examples of Recursion, in Artificial Intelligence and Mathematical Theory of Computation, Papers in Honor of John McCarthy, (ed. Vladimir Lifischitz), pp.207-230, Academic Press (1991). この論文の中にニセ竹内関数とういうのが出てくる。Lispの生みの親として名高いジョン・マッカーシー教授が1978年、前に出てきた佐藤雅彦さんと一緒に、私のいた研究所に来たとき、タライ回し関数のことを聞いて面白がり、それを米国の仲間たちに広めてくれた。しかし、ちょっとした記憶違いで(※7)、elseのうしろの y を z にしてしまったものである。こちらの計算の手間はずっと小さくなる(写真1)。

写真1:マッカーシー先生と佐藤雅彦さんが、私の説明を聞いている場面。その後、マッカーシー先生が私に手紙を送ってきてくれた。この関数がお前の作ったものなら、ちゃんとこの再帰関数がちゃんと定義できている、つまり停止することを証明せよ、という内容だった。その手紙についていたメモ(写真2)
が、なんと当時スタンフォード大学で同僚だったクヌース教授が開発した文書清書システムTeXを彼が初めて使って書いたものだった! どうも今回の話、同一人物が何度も出てくるというか、再帰している。
※7:実は記憶違いではなく、使った引数を全部使わないことがあるのは変だと思ったという理由による。
竹内先生への質問や相談を広く受け付けますので、編集部、または担当編集の風穴まで、お気軽にお寄せください。(編集部)
変更履歴:
2015年05月01日:tarai 関数の定義を画像(TeXで整形したものをキャプチャ)に置き換えました。表示環境によってインデントが揃わない場合があったため。
2015年05月04日:野崎昭広先生の「詭弁論理学」「逆説論理学」を、「岩波新書」としていましたが、正しくは「中公新書」でした。大変申し訳ありません。お詫びして訂正いたします。
2015年05月31日:脚注4で、野崎昭広先生の著書を「計算機のための数学」としていましたが、正しくは「計算機数学(共立数学講座 11)」でした。大変申し訳ありませんでした。お詫びして訂正いたします。ご指摘いただき、ありがとうございました。
SNSシェア







