ハッカーの遺言状──竹内郁雄の徒然苔
第32回：試験問題を作る

第18回の遺言状で問題を作りまくる「問題児も悪くない」という話を書いたが、学校の先生をやっていると問題児じゃなくとも、試験問題を作らなくてはならない。そもそも学生にとって試験は、自分の将来を左右しかねない重いものである。個々の試験はそれほどでないにしてもチリも積もれば重くなる。

試験のときに初めて先生の名前を意識するというか、思い出すというか、そういう学生がいる（※1）。だから、講義のときよりも試験のときのほうが教員にとって「勝負感」が強い。そう考えない教員が多いかもしれないが、試験問題の作成は実は結構独創性が求められる高度な知的作業だと思う。

そういえば、大学以外の場所で研究者として活動してきた人が、大学で非常勤講師などして試験問題を作るとほとんどの場合難しくなりすぎる。これも、「勝負感」が強く出て、つい頑張ってしまうからである。もっとも、こちらのほうは、自分が苦労して構成した講義の内容がちゃんと学生に理解してもらえているという錯覚に基づく場合が多そうだ。ベテランになるとそういう錯覚は持たない。

まだ大学院修士課程のころ、先生に言われて津田塾大学の何たらという計算機関係の科目の演習に動員された。それが大学というところで教壇に立った最初である。何を教えた（？）のかさっぱり覚えていない。不細工とはいえ、若い男が教壇に立っているのだから、学生たちの間にはいろいろあったらしい。見事な視線検知が行われていた。「誰それを見ている割合が高い」など。

閑話休題。NTTの研究所に入ってから今日に至るまで、いろいろな大学で非常勤講師をした。私の履歴に書いてある本来の学校以外では10校ほどで集中講義や半期の講義をしたことになっている。集中講義では試験はほとんどしていない。大体はレポート出題である。実際、集中講義で試験をするのは学生に酷である。レポートは真剣勝負とはほど遠いが、実は学生のレベルは意外とよく分かる。文章力はもちろん、どれだけ関連分野を勉強していたかが自ずと滲み出る。レポートを読むのはそれなりに大変だが……。

で、半期も連続で講義した科目を、レポート提出ということにはやっぱりしない。学生もレポートのほうが楽だと思っている。本当に厳しいレポート課題だと、それはちょっと違うと思うが……。

前置きが長くなったが、こういう背景説明は試験問題を作るという話題のときは必要な気がする。

レポートでも試験でも同じことだが、相手は大学生。過去問データベースが結構整備されている。だからまったく同じ問題はもちろん、ちょっとだけひねった問題でも出すのに逡巡する。もっとも過去問を勉強してくるくらいの学生だったら、もうそれだけでも合格にしてもいいような気もするが。

ということで、冒頭の「独創性を発揮した試験問題」に話は戻る。NTT研究所から電通大に移って、それまでよりも真面目に試験問題について考えることになった。それ以前から電通大でも、津田塾でも試験はしていたのだが、ブルッと身震いしたとでもいうのだろうか。しかし、経験があったにもかかわらず、電通大での当初は難しい問題を作りすぎてしまった。身震いして、汗やら火花が飛び散ったのか……。

試験問題では「識別性」がとても重要である。識別性には資格試験のような、受かる、受からないの2つに分けるのもあるが、順番をつけるために、成績の良い悪いがなだらかに差がつくことに意味があるものがある。後者の場合、得点分布（何人がどの点をとったかの分布）が0点から満点までなるべく平坦に分布しているのが理想的だ。

あるとき意を決して、得点分布を平滑にすることに激しくこだわった問題作りをしたことがある。その結果は以下の通りである（図1）。

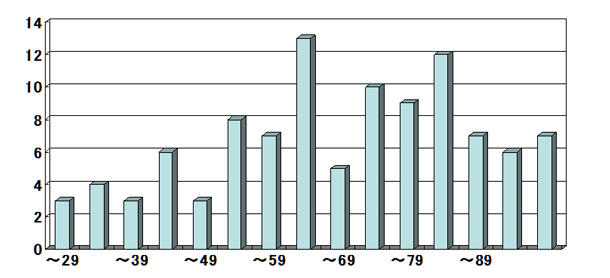
図1：「得点分布を平滑にすることに激しくこだわった問題作り」の結果

可と不可の境である60点のところに妙なピークがあるのは、仏心を起こしてギリギリ救済した学生が少しいたからである。これは私の史上最高傑作の得点分布である。

そのころから私は某試験センターのお手伝いをすることになったのだが、この試験は得点分布による識別性が特に重要視されるところであった。サンプルの母集団は巨大なので、統計分析は万全である。小問ごとの正解率や誤回答選択率が厳密に計算され、問題の「識別性の品質」が評価される。やさしすぎても難しすぎてもダメ。極端な話、全員0点でも全員満点でも、問題として意味がない。

なお、ここで一様に平滑というより、ラクダの背中のようなフタコブ分布も良いとされることも知った。分かっている層と分かっていない層の分離がよく分かるからである。

某センターでは、科目選択で不公平が起こらないように、どの科目も平均点が60点になることが求められている。でもこれは、はい、承りました、と言うほど簡単ではない。難易度調整はコンピュータゲームだったらテストプレイを通じてモニターの意見を聞けるが、こればかりは厳重な情報統制の中で出題者自身が塩梅するしかない。某センターだけではない。クラスの小テストから、期末試験、入学試験まで、これはすべてに共通する。学生の身にどこまでなれるか、つまり相手をどこまでシミュレートできるかという話になる。

良い得点分布を達成するコツは、問題を複数の小問に分け、段階的に難しくなるように作成することである。受験者にとっても、順次解けていくので、「やった進行感」がある。しかし、これも言うはやさしいが、難しい。

難易度調整ばかり気にしていると、それを抜け出したくなることもある。世界最大の計算機学会ACMが主催しているACM学生プログラミングコンテスト（ACM ICPC）は、試験ではないかもしれないが、閉じた会場で制限時間内に答えを出さないといけないので（3人のグループとはいえ）限りなく試験に近い。

大昔の話だが、私はACM ICPCの審判団に入って、出題のお手伝いをしたことがある。「受験者」は選びぬかれた強者たちである。これは5時間で8題を解いていくルールなので、難易度順に問題が並べられる。それもあって、後半向けに、つい意地悪な問題を作りたくなってしまった。まず動的なデータ構造を使わないと辛いうえ、いわゆるゴミ集め（Garbage Collection）がない言語だと使わなくなったメモリを自分で回収するなど、メモリ管理に気を遣わないといけないことを前提にするのである。この程度の基準を考えたからといって、簡単に問題が浮かんでくるわけはない。

こういうときに役立つ、思考のための時間が教授会である。紙とボールペンで、有名な3n+1問題（※2）をちょこちょこいじっていたら、ダイナミックに形が変化していく、面白そうな生命体のようなものができあがった。天地創造の神様のような気分である。ナンバーとアミーバを融合して「ナミーバ」（numoeba）と命名した。Lispだったら簡単にプログラムが書けるのだが、通常の言語だったら、メモリ管理や算術演算オーバーフローなどの心配をしないといけないので、問題自身は微妙に妙な言い回しが必要になってしまった。審判団でいろいろ調整して8題の最後のほうに出題したが、正解者はゼロだった。難易度が高すぎたようだ。いくら欲求不満解消のためとはいえ、やっぱり張り切りすぎてはいけない。

ナミーバについては、NTT研究所の後輩、佐藤進也君（現在、日本工業大学教授）が実にあの手この手で調べてくれた。ナミーバを動画で見ることのできるプログラムが

http://www.shin-ya.org/numoeba

から入手できるので、ぜひお試しあれ。ナミーバの規則は、このページからリンクされているACM ICPCの過去問（英語）、あるいは下のほうにあるプログラミングシンポジウムの佐藤君の論文（日本語）に記載されている。それが面倒な人のために、ぐにゃぐにゃと動き、そのうち死んでしまうナミーバの動画をYouTubeで公開してもらった。Collatzの予想が正しければ、永遠に生き続けるナミーバはいないはずである。

ちなみに、そこからリンクされている佐藤君の「制約より生じる調和──謎の算術生命体ナミーバの組織化」では、生命体に独特の1/f ゆらぎがナミーバに現れるように奮戦した面白い記録が書かれている（上記のナミーバでは1/f ²のゆらぎが現れる）。興味のある方はご一読願いたい。

短時間で答えを出させる試験というのはある意味いい加減なものだ。その人の本当の実力が正確に現れるわけではない。

第28回の走馬燈で書き洩らしたが、私、実はかれこれ50数年前の中学2年生のころ、四角四面の菱という名前の先生に誘われて計算尺クラブなるものに属していた。

今どきの人は計算尺自体をご存知ないかもしれない。私が使っていたのは（私にとっては当然意味不明の）特殊関数などのない平凡な計算尺だったが、ヘンミというメーカーの製品である。昔の画像ぐらいはあるだろうと検索したら、何とヘンミ計算尺株式会社は今でも存続している。存続しているどころか、計算尺という名前が残っているのが不思議なくらいのハイテク企業になっている！　正直、本当に驚いた。

http://www.dentaku-museum.com/hc/computer/sliderule/sliderule.html

それにしてもヘンミが日本の計算尺の98％、世界の70％のシェアだったというのは今日初めて知った。湿気による伸縮がほとんどない孟宗竹はすごい！　実際、本当に精密な道具だった。

それはともかく、ソロバンと同様、検定試験というものがあり、三角関数などが出てくる2級以上は中学生には無理で、掛け算・割り算だけの計算のスピードと正確さ（※3）を検定する3級と4級の受験が相応しい。3級と4級の違いがどこにあるのかもう記憶にないが、3級だと計算尺の真中の尺（スライド）の動き（滑べらせ方）をある程度知的にやらないといけないし、小数点の位置の暗算が面倒だったように思う。

受験の日、私はダメ元で3級と4級の試験を両方受けた。結果は、4級不合格、3級合格であった。まさに試験というものの解像度の悪さが象徴された事件だった。しかし、これでも私は計算尺3級と名乗れるのだろう。でも、計算尺に慣れ親しんでいたおかげで対数の理解は一瞬であった。

日本には受験戦争という言葉があるくらいに、入学試験が子供たちの成長の節目節目に影を落している。聞くところによると韓国も大変だ。それに比べると、米国に「受験戦争」という概念はない。私の義理の甥っ子2人の育ちを聞くと、なるほどそれは本当だと思う。

何回かご紹介したように、私は2011年から3年間、年に4カ月強、エジプト日本科学技術大学というところで、毎年数名ずつだったが、エジプト人の大学院生を相手に教鞭（というより強弁のほうが相応しい？）を振るった。

エジプトの試験事情は日本よりさらに厳しい。情報処理学会のコンピュータ教育関係の論文誌に、そのあたりを書いたので、それを遺言状的（？）に噛み砕いて紹介し、その中で私がどんな試験をしたかを紹介しよう。

エジプトには18の国立大学があり、10世紀に設置された宗教系の1校を除いては、すべて総合大学である。あとは外国系の私立大学が18校。国立大学は授業料が無料化されていて、かつ、エジプトの8200万の人口の60％が35歳以下（33％は14歳以下なので、典型的なピラミッド型の人口構成）という若い国であることから、マスプロ教育が常態化している。カイロ大学が学生数26万人、それに次ぐアレクサンドリア大学が18万人である。日本最大級の大学でも5万人だ。

少人数教育を謳う私立大学は授業料が高額なので、富裕層の子弟しか入れないうえに、大学院が充実していない。つまり、エジプトでは無料でマスプロ教育を受けるか、高額の授業料で学部までの教育を受けるか、の二者択一のようだ。

理系を目指す子供は日本でいう中学から高校へ進学するとき、まず大学進学を目的とする統一テスト（サナウエーアンマ）が受験できる高校と、技術習得のための工業高校とに学業成績によって振り分けられる。工業高校を出たらテクニシャン、高校から工学部に進んで卒業すればエンジニアとなる。この2つの言葉は厳密に階級差を表すために使われている。

高校では進級のときに、工学部受験コース、医学部・理学部受験コース、文科系受験コースに分かれる。医学部と理学部が一緒になっているが、成績優秀者だけが医学部に行ける。理学部はその落ちこぼれ。

高校3年のときにサナウエーアンマを受験して、成績順に最終的な振り分けが行われる。大学入試は存在しない。本当に一発勝負なので、日本のセンター試験よりずっと恐い試験である。サナウエーアンマが一生を定めるとも言えるので、裕福な家庭の子供に対する教育投資熱は日本以上のものがある。

エジプトには職業別の国家試験がなく、大学卒業がそのまま職業資格になる。工学士はエンジニアのシンジケートに入り、そこからエンジニアであることの証明書を発行してもらう。このシンジケートはエンジニアを経験年数などでランクづけする。こうして社会が回っている。

ここまで見ても、入学試験というより、普段の試験の重みが大きいことが分かる。

さて、私の講義はプログラミングの理論的基礎を学ばせるという性格のものであった。といっても、がちがちの理論ではなく、むしろ考えさせること重点に置いた塩梅である。どうもマスプロのエジプトの大学学部では考えるではなく、詰込み教育らしい。だから、パズルの出題などエジプトの学生には未体験の講義になったと思う。

学生は数人なので、寺子屋風、対話的に講義を進め、レポート問題も時おり出して、手を動かすことをやってもらっていたのだが、試験となると事情は一変する。試験の成績が悪いと奨学金や将来の地位に明確に悪影響が出る。

それを知りつつ、私はまた「試験問題作り」で独自路線をやってしまった。「自分の頭で考える」がモットーなので、講義スライド、ノート、教科書、PC何でも持ち込み可能にするかわりに、講義の中では言及しなかったようなオリジナルの問題を出したのである。知識詰め込み教育の完全なアンチテーゼだが、講義の中でポイントとなる部分を本当に理解していれば解ける応用問題である。「そのポイントについて言及してくれ」と、最後の講義ではリクエストが連発したので、それも漠然と教えた。まさに至れり尽くせり、である。

学生部屋で行う寺子屋型試験なので（写真1、写真2）、私が常に動き回って解いている過程を観察することにした。すると、案の定、応用問題の経験があまりないのか、学生の手が止まりがちである。このままでは奨学金返上の成績になってしまう。

写真1：女子の試験部屋。イスラム教の戒律がエジプトでは少し緩いことが分かる。そういえば3人とも子供がいる。

写真2：男子の試験部屋。

ここで私は覚悟を決めた。試験時間は帰りの通勤バスが出るまで、無制限延長。そのかわり、自分で考えて解けるまで頑張るように、と宣言した。それでもダメなものはダメなので、個々の学生の答案進行状況を見ながら、個別に考え方のヒントを漏らす。間違った答えを書いていたら、指さして 「そうなの？」と指摘する。ほかの学生にも聞こえるので、言い方には格別の工夫が必要だったが、何とかなった。こうして、全員が75％以上の正解率が得られるまでサポートした。このようにしても、75％止まりの学生もいれば、啓示があることによって95％以上の正解に達する学生もいた。それが普段の講義やレポートで感じていた成績差をほぼ正確に反映していた。

こうして1時間半の試験に3時間以上かけてしまったが、学生たちの反応は最高だった。それは安心の成績が取れたことよりも、試験の場で初めて目からウロコが落ちたような理解ができたことの喜びであったと信じたい。試験の終わりに先生と握手するなどという風景は滅多になかろう。

日常とは異なる、アドレナリン出まくりの真剣勝負の試験時間に、理解が突然・急激に深まるという体験をさせることは、非正規だとは思うが、意外に有効な教育法かもしれない。ただし、寺子屋規模でないと無理だろう。

こうやっていろんな試験で学生たちを苦しめてきた報いは、遺言状を書き終えて、閻魔さまの前で行う口頭試験のときに巡ってくるのだろう。しょうがないか。（つづく）

※1：答案用紙に教員の名前を書かないといけないからである。
※2：3以上の任意の奇数から始め、以下を繰り返す。
(1) 数が奇数だったら3倍して1を足す
(2) 数が偶数だったら2で割り切れるあいだ、2で割る
そうするといつかは数が1になる。そこでおしまい。これはCollatzの予想と呼ばれていて、もう80年近くも証明ができていない難問である。
※3：計算尺は目盛で数値を設定したり読んだりするので、どうしても誤差が出る。有効数字は3桁。

竹内先生への質問や相談を広く受け付けますので、編集部、または担当編集の風穴まで、お気軽にお寄せください。（編集部）

この記事を、以下のライセンスで提供します：CC BY-SA
これ以外のライセンスをご希望の場合は、お問い合わせください。