プラレールで半加算器を設計した話

はじめまして、サイボウズ・ラボユース第5期生の赤間です。ラボユースでは構文を自由に拡張できるプログラミング言語の開発を行い、今年の3月に卒業しました（※1）。

このたび、以前から構想していた「プラレールで論理回路を設計する」という挑戦の一環で「半加算器」という論理回路の素子を設計して、サイボウズのオフィスに構築しました。

そして、こちらが完成したプラレールによる半加算器です（写真1）。総レール数「209本」、橋脚「178個」を使用し、定価換算の総工費は「5万3900円」でした。

写真1：プラレール半加算器の全体像

この記事では、プラレールによる論理回路設計の基礎および半加算器のメイキングを紹介します。

ご存知の方も多いと思いますが、プラレールはレールを組んで電車を走らせて遊ぶ、タカラトミーから発売されているおもちゃです。レールの種類には、直線や曲線、分岐やスロープなどがあり、立体的かつ技巧的なレイアウトを組むことができます。そのおかげで、意図せずに論理回路設計が可能になってしまいました。

半加算器とは

半加算器は、コンピュータで2進数の足し算をするための基本的な論理ゲートです。これは1bitの2進数を2つ受け取り、この2つの数を足した2bitの2進数を出力します（※2）。入力をそれぞれ「A」「B」、出力の2進数の上下の桁を「C」「S」とすると、表1のように計算できます。

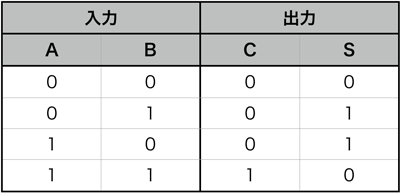
表1：半加算器の入力と出力

プラレールで2進数を表現する

それでは、プラレールで0と1を表現する方法について説明していきます。

プラレールで論理計算をさせるという試みには、すでに私とは別の先駆者がいます。

こちらの動画では、プラレールのほかにレゴブロックによるギミックを用いて、論理計算の仕組みを分かりやすく説明しています。

本稿で紹介するプラレールの論理回路構成とは、0と1の表現など基本的なことは共通していますが、純粋にプラレールのみを用いて複雑な論理回路を構成しているという点で異なっています。冒頭にお見せしたレイアウトがかなり複雑になっていたのは、プラレールだけで構成する工夫をしたためです。

プラレールで2進数

さて、プラレールの世界には「ターンアウトレール」という興味深いレールがあります。このレールは、黄色いポイントの方向によって、電車が進む方向を分岐させることができます。たとえば、ポイントが曲線方向を向いていたら、電車も曲線の方向に進みます。

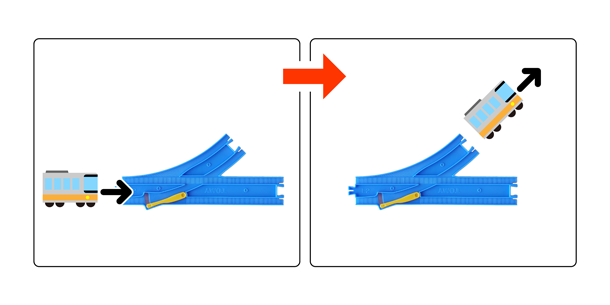
図1：曲線方向にポイントが向いていると電車は曲がる方向に向かう

また、逆方向から入ると、ポイントを蹴って方向を変えることができます。

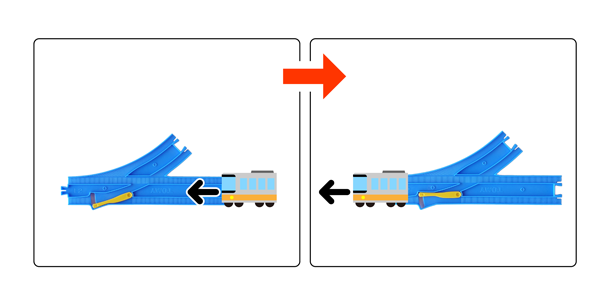
図2：ポイントを電車の車輪が蹴って向きを変える

このターンアウトレールのポイントを0と1に例えてみましょう。直線方向を0、曲がる方向を1だと考えると、なんと0と1をプラレールに記憶させることができます！　ヤッター！

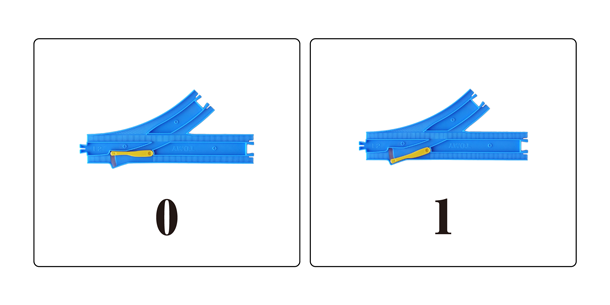
図3：プラレールで「0」と「1」を表現

readとwrite

もちろん人間が直接ポイントを操作して0と1の値を設定したり、目で見て読み取ったりすることもできるのですが、これらの操作をプラレールの電車に行わせるとプログラムとして発展していきそうです。

まずは、ターンアウトレールに格納された0か1の値のread（読み取り）を電車にさせてみましょう。これは簡単で、図中のA点から電車を走らせることで、向かう先のレールが変わります（図4）。ターンアウトレールのポイントの向きによってプログラムが条件分岐をするイメージです。

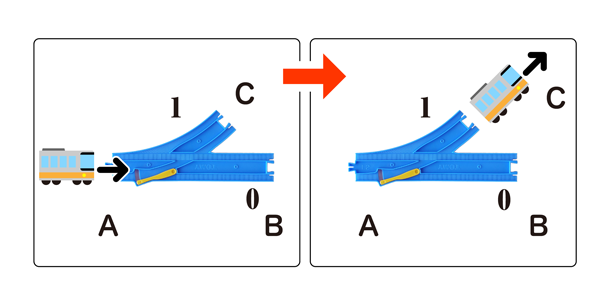
図4：ターンアウトレールに保存された値の読み取り

次に、write（書き込み）ですが、これはreadとは逆側の端から電車を走らせます。直線方向から来た場合は、電車はポイントを直線方向（0の方向）になるように蹴り、曲線方向から来た場合は、ポイントを曲線方向（1の方向）になるように蹴ります（図5）。これで書き込みもOKです。

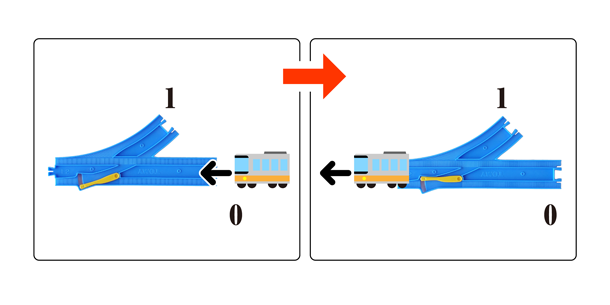
図5：ターンアウトレールへの値(0)の書き込み

これらをまとめると、電車の出入りする端点と方向によって、次のような機能を持ちます（図6）。見事にメモリセルと対応していますね。

図6：ターンアウトレールに対する操作一覧

NOTとORとANDゲート

それでは、実際にプラレールで基礎的な論理ゲートを作ってみましょう。入力用のターンアウトレールにあらかじめ設定した値（AおよびBと名付けます）を電車が読み取り、出力用のターンアウトレール（Xと名付けます）に電車が値を書き込むという想定です。ここで大事なのは、電車はCPUでいうところのプログラムカウンタに相当するということです。なので、プログラムのエントリーポイントにあたるレールから電車を走らせることで、論理演算を開始します。

まずは、一番簡単な「NOT」（X = ¬A）。直線と曲線を逆にしてつなぐだけなのでこれは簡単です（図7）。実際に電車の動きをなぞってみると、「A = 0」なら「X = 1」に進入し、「A = 1」なら「X = 0」へ進入することでXのポイントの向きを切り替え、値を書き込むことが分かります。

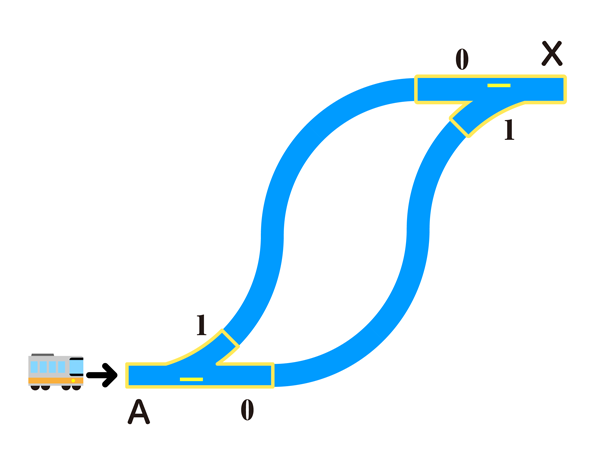
図7：プラレールによるNOTゲート

次に、「OR」（X = A + B）です。これは合流用のターンアウトレールを1つ追加することで実現ができます（図8）。Aが0ならば次にBを読み取り、Bが0ならば出力Xに0を書き込み、Bが1ならば出力Xに1を書き込みます。そしてAが1ならば、Bの値を参照するまでもなく出力Xは1になります。ここで、Xに1を書き込む場所が2カ所あるため、ダミーのターンアウトレールを追加し、2つのレールを合流させています。

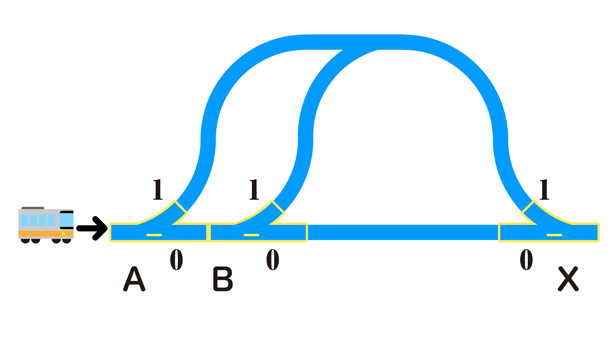
図8：プラレールによるORゲート

そして、「AND」（X = A ⋅ B）はド・モルガンの法則により、ORの0と1を逆転させれば作成できます（図9）。ちょっと曲線が多くなりましたが、本質的にはORと変わりません。

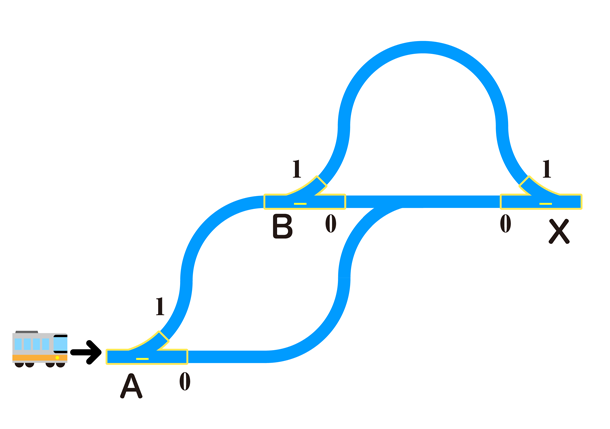
図9：プラレールによるANDゲート

XORが作れない！？

さて、これでANDとORとNOTがプラレールで表現できると分かったので、任意の論理関数が実現できるはずです。察しの良い方なら万能性を持つNANDゲートを作成すればもう十分だと考えるかもしれません。しかし、プラレールの世界ではAND、OR、NOTもしくはNANDを組み合わせても設計できない論理ゲートが存在します。そう、排他的論理和（XOR）とその否定（NXOR）です。

これは本質的には、同じ変数を別々の場所で読み取ることができないことに由来しています。さて、このことを解説するために、プラレール回路をプログラムとして解析する準備をしていきます。

プログラムっぽく見ると

それでは、プラレール回路を解析するために、プラレールの回路をプログラムとして考えてみましょう。

ターンアウトレールからの値の読み込みでは、変数の値によって進む先のレールを振り分けることができるので、これはプログラムの条件分岐とみなせます。逆に言うと、プログラム中のどこから変数を参照したとしても、条件分岐先は0と1それぞれに1カ所しかありません。つまり、1つの変数を読み取った値を複数の場所に持ち出すことができません。

また、ターンアウトレールへの書き込みでは、0か1の定数を書き込めますが、書き込んだあとに一本のレールに合流してしまいます。つまり、書き込んだ先に向かう方向はただ1つなので、無条件ジャンプと同じことが起こります。

以上をまとめると、次のようになります。

・どこからでもreadできるが、0と1それぞれの場所にジャンプする。
・どこからでもwriteできるが、書き込んだあとに1カ所にジャンプする。

では、これらの制約を持つプログラムをプラレールプログラムと名付けて、C言語風の構文でANDおよびXORのプログラムを書いてみます。

ANDとXORのプログラムの違い

ANDを表すプラレールプログラムは次のようになります。入力はAおよびBとして人間が手入力することを想定し、出力はXとします。

このように、プラレールプログラムでは、AやBなど、同じ変数の値を1カ所のif文でしか読み出せず、Xに書き込むときに、必ず同じラベル（たどり着く先のレール）にしかジャンプできません。ANDのプログラムは、この制約を破らずに書くことができます。

続いて、XORを愚直に作成すると、以下のプログラムになります。問題点に気付いていただけるでしょうか。

XORのプログラムでは、入力変数Aの値を「*」で示した2カ所で読み出しています。つまり、XORのプログラムでは本質的に値のコピーが必要になってしまいます。そしてこの問題は、変数Aの値を2つに複製することで解決します。そのために自動ターンアウトレールというレール部品を導入します。

自動ターンアウトレール

プラレールには、「自動ターンアウトレール」という素敵なレール部品があります。普通のターンアウトレールと違うのは、レール内部のバネ仕掛けでポイントを制御しており、電車が通るごとにポイントの方向が自動的に逆方向へと切り替わることです。これはトグルスイッチのように働き、1回目に通ったときと2回目に通ったときで処理を変えることができます。

なお、普通のターンアウトレールと異なり、バネ仕掛けの都合上、自動ターンアウトレールへの書き込みはできず、逆方向から電車が進入してもポイントの向きを保持します。そのため、ポイントの方向を変更できるのは、電車がポイント方向から進入したときに反対側に切り替わる作用でのみです。

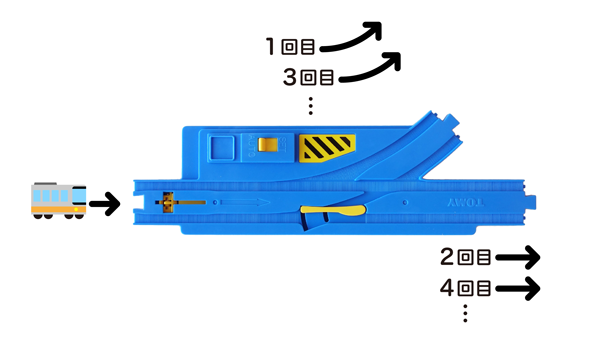
図10：自動ターンアウトレール

自動ターンアウトレールの合流機能

さらに、自動ターンアウトレールには、行き先を固定するモードもあります。これは、ポイントの側から入った電車を必ず直線方向（または曲線方向）に進ませるというもので、ターンアウトレールでは実現できない機能の1つです。これを用いることで、ターンアウトレールに対するreadとwriteを分割し、互いに影響を与えないようにできます。そのため、書き込みや読み込みをどこからでも行えるようにできます（ただし、合流する先は1カ所です）。

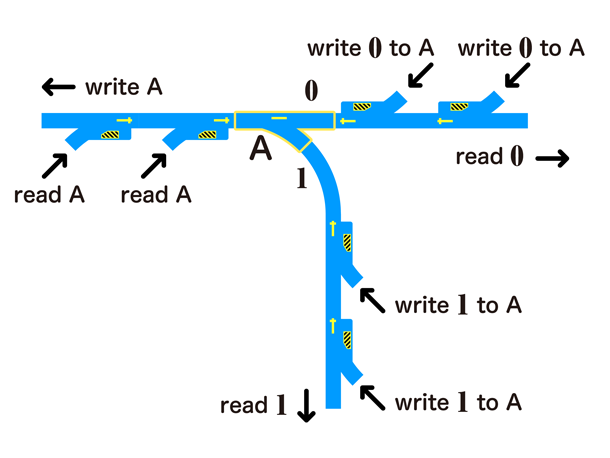
図11：自動ターンアウトレールの固定モードを使用してreadとwriteを分割

ちなみに実際の半加算器では、自動ターンアウトレールを直接使用するのではなく、ターンアウトレールの黄色いポイントを取り外すことで直線方向にしか進めないように改造したレール（写真2）を、コストやレイアウトの自由度のために使用しました。

写真2：自動ターンアウトレールの代わりに使用した「改造レール」

入力の複製をしてXORを構成

さて、自動ターンアウトレールを用いて、Aのコピーを2つ作成することを考えます。Aを読み出して、「A = 0」だった直後と「A = 1」だった直後の2カ所に自動ターンアウトレール「T0」「T1」を挟みます。そして、新しく中間的に用いる論理変数（ターンアウトレール）「R0」「R1」を導入し、R0およびR1に、Aの値をそのままコピーする方向に配線します。また、各自動ターンアウトレールT0、T1の初期設定は、曲がる方向（R0に向かう方向）が1回目とします。

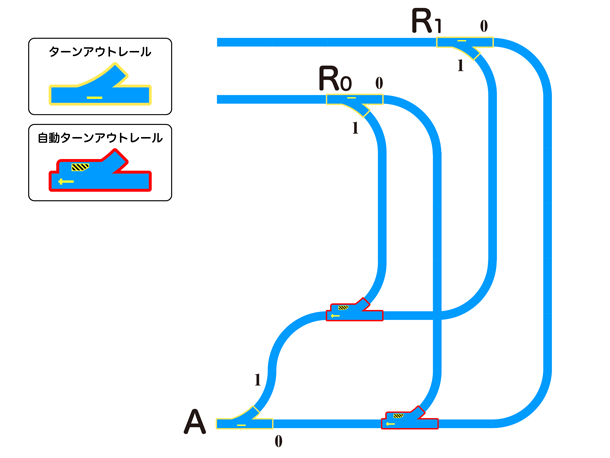
図12：AをR0、R1に複製する

すると、Aと同じ値を持った変数が2つ用意できたので、いよいよXORを構成します。

まず、R0に書き込んだあとは、2回目のAのreadが必要なので、Aのポイント側に接続します。次に、R1に書き込んだあとでBを読み取り、「B = 0」ならばR0を読み込み、「B = 1」ならばR1を読み込むことで、A、Bの値の組み合わせによって4分岐させることが可能です。

このときに、最初にR0、R1に書き込んだ方向とは逆方向に読み込みを行うため、readした行き先をwriteの書き込み元と分割するため、合流用の自動ターンアウトレールを合計4つ、曲がる方向に固定してそれぞれの分岐に挟みます（図13では矢印で合流を表しています）。そのあとに、出力を「X = 0」とする組み合わせのレール（「A = 0, B = 0」と「A = 1, B = 1」）を合流させ、「X = 0」を出力とするレールも同じように合流させたあとに、出力Xに書き込みます。これでXORが構成できました。

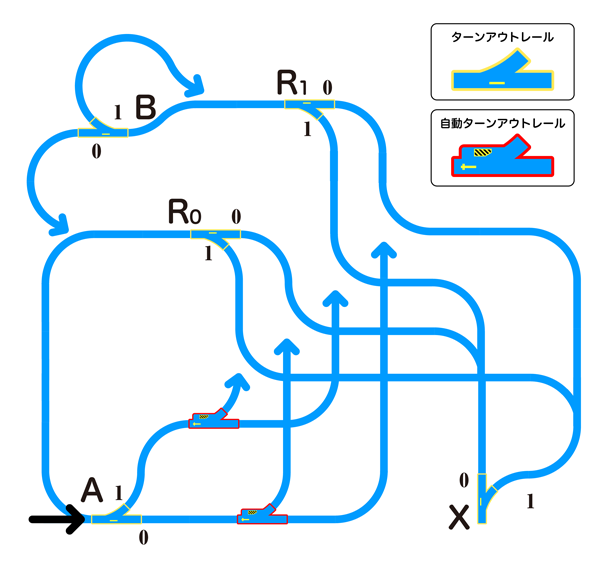
図13：XOR回路の接続関係

もしかすると、図で描くよりも、むしろプログラムの方が分かりやすいかもしれません。次のようになります。

XORから半加算器へ

それではいよいよ半加算器を構成していきます。半加算器の式は、

S = A ⊕ B
C = A ⋅ B

と表されます。AとBの値は、XORとANDで複数回参照されるため、値の複製のための自動ターンアウトレールは合計6個必要となります。

プラレール回路で重要なのはターンアウトレールなど各回路素子の連結関係だけなので、まず論理的なトポロジーを考えてから物理レイアウトに落とし込むのがセオリーです。そのため、先にトポロジーを書いてみます。実際に手書きで設計した図がこちらになります（図14）。

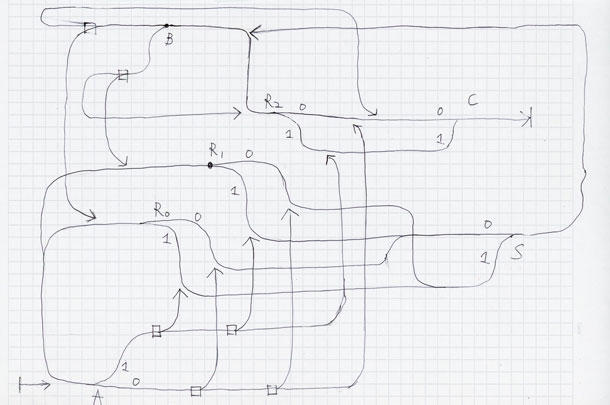
図14：実際の設計図（手描き）

この論理的なレイアウトに従って、実際のプラレールのレイアウトの設計図に“職人芸”で落とし込んだのが図15、図16、図17です。

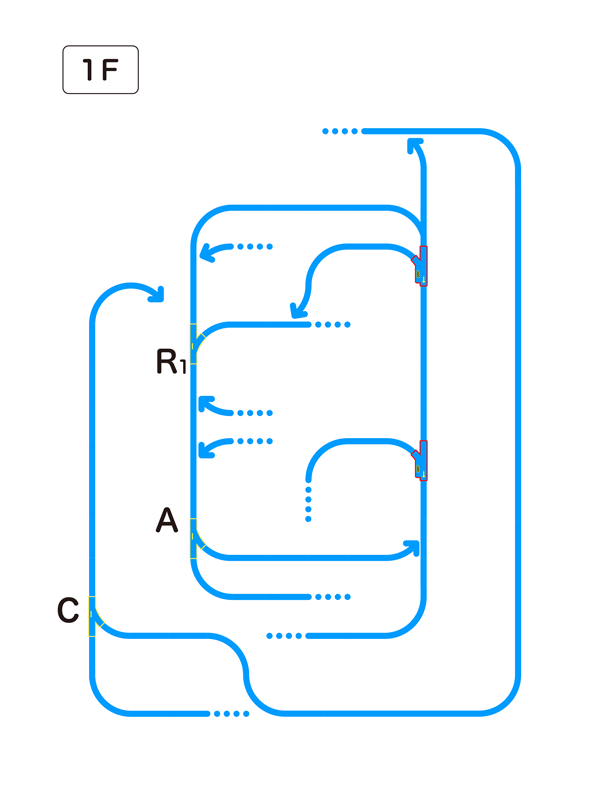
図15：プラレール半加算器の論理レイアウト図（1F）

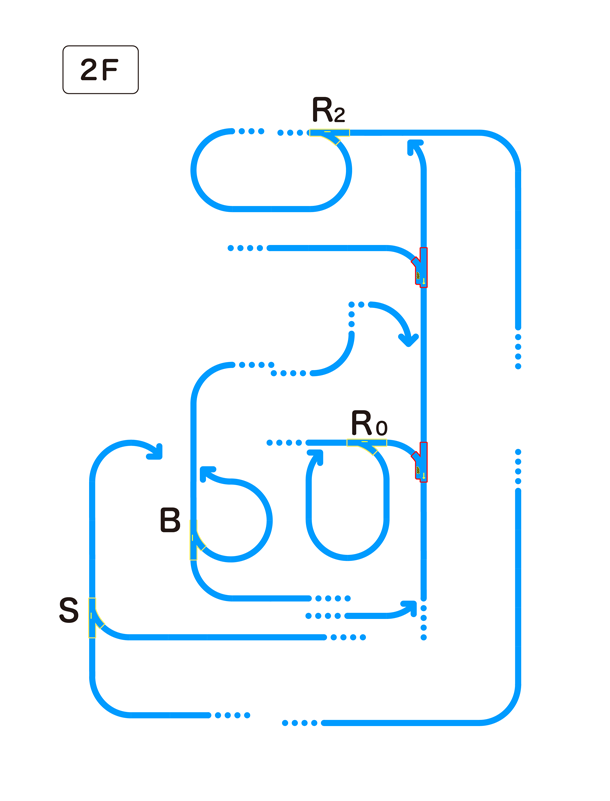
図16：プラレール半加算器の論理レイアウト図（2F）

図17：プラレール半加算器の論理レイアウト図（3F）

この図に従ってプラレールを組んでいきました。実際の組立作業は3時間ほどかかりました。

全加算器は？

ところで、半加算器を作ったら全加算器や複数桁の加算器も作りたくなりますよね？というわけで、実際に作ったらどんなことになるか簡単に試算しました。

論理回路では、全加算器は半加算器2つとORゲート1つで構成できます。プラレール回路でも同じことが言えますが、2つの半加算器間の値の受け渡しとなるインターフェイスがいくつか必要となり、単純に倍にはならず、ORゲートを追加するだけでも多くのレールを必要とするため、半加算器の3倍の規模になるだろうと予想しています。つまり、レールは600本以上必要で、総工費は約15万円になると見込んでいます。

さらに大雑把な計算をすすめると、nビット加算器は全加算器をn個使うため、総工費は「15 × n万円」、レールは「600× n本」以上は確実に必要だろうと予想します。例えば、8ビットの加算器なら4800本以上のレールを使用し、費用は120万円以上という一昔前のワークステーションみたいな金額になりそうです。

また、プラレールを計算アーキテクチャとして見た場合、速度も気になります。各入力に対しての計算時間を計測すると次のようになりました。テストに使用した車両は「S-02 ライト付500系新幹線」で、電池は満充電された「eneloop pro」を使用し、3回計測した中央値を記録しました。

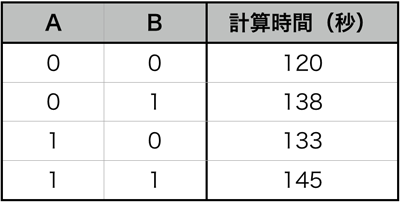
表2：プラレール半加算器の計算速度

おわりに

プラレールによる論理回路はまだまだ発展段階です。さらに複雑なプラレール回路を実装できる可能性もありますが、現在の設計手法が冗長であることも考えられます。本稿で解説した半加算器も、さらにコンパクトなレイアウトで表現できるかもしれません。挑戦者求む！（了）

※1：「ユーザが構文を自由に変更できるプログラミング言語」（赤間 仁志、2016）
※2：ちなみに全加算器という回路もあります。これは3つの1bitの2進数を受け取り、その和を2bitの2進数として出力します。これを連結させることで任意桁の2進数の加算回路が構成できます。

読者の皆さんからの、ご意見、ご質問などを、広く募集しています。編集部、または担当編集の風穴まで、お気軽にお寄せください。（編集部）

変更履歴：
2016年11月03日：図13に誤りがあったので修正しました。「B」の分岐のところの0と1が逆でした。また、そこから伸びる矢印が曖昧でしたので、はっきり分かるようにしました。この図で迷われた皆さま、申し訳ありませんでした。

この記事を、以下のライセンスで提供します：CC BY-SA
これ以外のライセンスをご希望の場合は、お問い合わせください。